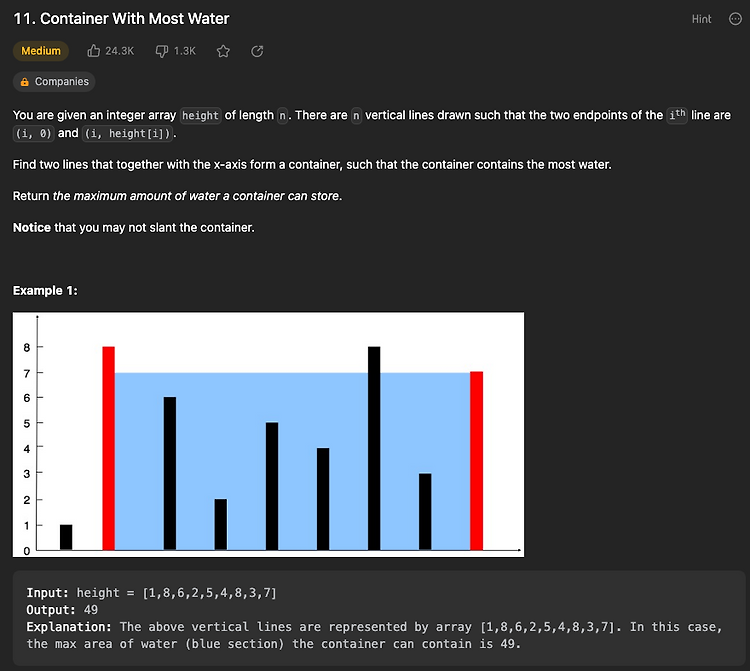
11. Container With Most Water
Description: Solution: Brute force method is not adapted as a solution. We are gonna make the pointer end of both array. Shift l if height[l] is smaller than height[r]. Else: shift r to right.
Description: Solution: Brute force method is not adapted as a solution. We are gonna make the pointer end of both array. Shift l if height[l] is smaller than height[r]. Else: shift r to right.
Description: Solution: We need to nums.sort() before moving pointer. i is a count, a is the value (enumerate) if i > 0 and a == nums[i-1] => if i is bigger than 0, we make sure not using same value l, r pointers to find the two sum for 0 of three sum. Since we sort the values, if threeSum is bigger than 0, we should move r pointer to left. elif threeSum is smaller than 0, we should move l pointe..
Description: Solution: We are gonna set l, r, m pointers to find in O(logn). If l pointer value is less than m pointer value: target should be between l and m or between m and r. if target is more than m value or target is less than l value, we are gonna see right portion, except left portion. else we are gonna see left portion, except right portion. If r value is less than m value: target can b..
Description: Solution: I set the right and left pointers to the end of the array. m is the pivot(first set the middle of the array). If m is more than l, then we can throw out the left portion. Now, the new l is the next value of m. Else, we can throw out the right portion, so the new r is the previous value of m. When we get the nums[l] is less than nums[r], we return the res.
Description: Solution: tmp will be used for curMin. Example: [-1, -2, -3] nums[i]= -2: tmp = 2, curMax = 2, curMin = -2 -> res = 2 nums[i] = -3: tmp = -6, curMax = 6, curMin = -6 -> res = 6 ※ Think about all negative integers array case!
Today, I solved "Maximum Subarray." Description: Solution: As we can see, we don't have to include the first negative array. curSum is a cumulative sum of numbers. If curSum is negative, it means that subarray is not for maximum sum. I use max() to compare the curSum and maxSub.
Today, I solved coin chnage. Description: In this problem, we should find the fewest number of coins that make up that amount. Solution: This is the brute force solution. Let's say coin is [1, 3, 4, 5], and amount = 7. dp[0] is always "0" (because no need to coin to get to 0) dp[1] = 1 dp[2] = 2 dp[3] = 1 -> one 3coin dp[4] = 1 -> one 4coin dp[5] = 1 -> one 5coin dp[6] = 2 -> one 1coin + one 5co..
Today, I solved the climbing staris. Description: Solution: Let's say the example(n = 5). On the 4th stair, we have only 1 way to get 5th stair. On the 3rd stair, we have (1 + 1) ways to get 5th stair. On the 2nd stair, we have (2 + 1) ways to get 5th stair. In my code, we set (n-1)th stair as "one", and nth stair as "two." We shift those one and two until we get to 0(start point). (n-1) and (n)..
Today, I solved "Reverse Bits." Description: In this problem, we are gonna do reverse order of 32-bits number. Solution: "output" will store "0" or "1." If the bit number is 1, then the output store 1 in it. Otherwise, it stores 0. In output, we shift the bit left, and also we shift the bit right in n.
Today, I solved the Missing number. Description: In this question, we are asked to find missing number in nums. Solution: In this method, we are gonna subtract sum of nums from sum of every number of n. For example 2: The length of nums: 2 Range: [0, 2] sum([0, 1, 2]) - sum([0, 1] = 2 Space Complexity: O(1) Time Complexity: O(n)








